Standard array

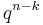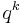In coding theory, a standard array (or Slepian array) is a $q^{n-k}$ by $q^{k}$ array that lists all elements of a particular 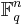$\mathbb{F}_q^n$ vector space. Standard arrays are used to decode linear codes; i.e. to find the corresponding codeword for any received vector.

1 Definition
2 Constructing a standard array
- 2.1 Construction example
3 Decoding via standard array
4 See Also
5 References

Definition

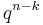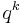A standard array for an [n,k]-code is a $q^{n-k}$ by $q^{k}$ array where:

The first row lists all codewords (with the 0 codeword on the extreme left)
Each row is a coset with the coset leader in the first column
The entry in the i-th row and j-th column is the sum of the i-th coset leader and the j-th codeword.

For example, the [n,k]-code 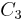$C_{3}$ = {0, 01101, 10110, 11011} has a standard array as follows:

0	01101	10110	11011
10000	11101	00110	01011
01000	00101	11110	10011
00100	01001	10010	11111
00010	01111	10100	11001
00001	01100	10111	11010
11000	10101	01110	00011
10001	11100	00111	01010

Note that the above is only one possibility for the standard array; had 00011 been chosen as the first coset leader of weight two, another standard array representing the code would have been constructed.

Note that the first row contains the 0 vector and the codewords of 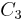$C_{3}$ (0 itself being a codeword). Also, the leftmost column contains the vectors of minimum weight enumerating vectors of weight 1 first and then using vectors of weight 2. Note also that each possible vector in the vector space appears exactly once.

Constructing a standard array

Because each possible vector can appear only once in a standard array some care must be taken during construction. A standard array can be created as follows:

List the codewords of $C$ , starting with 0, as the first row
Choose any vector of minimum weight not already in the array. Write this as the first entry of the next row. This vector is denoted the 'coset leader'.
Fill out the row by adding the coset leader to the codeword at the top of each column. The sum of the i-th coset leader and the j-th codeword becomes the entry in row i, column j.
Repeat steps 2 and 3 until all rows/cosets are listed and each vector appears exactly once.

Note that adding vectors is done mod q. For example, binary codes are added mod 2 (which equivalent to bit-wise XOR addition). For example, in 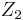$Z_{2}$ , 11000 + 11011 = 00011.

Note also that selecting different coset leaders will create a slightly different but equivalent standard array, and will not affect results when decoding.

Construction example

Let $C$ be the binary [4,2]-code. i.e. C = {0000, 1011, 0101, 1110}. To construct the standard array, we first list the codewords in a row.

0000	1011	0101	1110

We then select a vector of minimum weight (in this case, weight 1) that has not been used. This vector becomes the coset leader for the second row.

0000	1011	0101	1110
1000

Following step 3, we complete the row by adding the coset leader to each codeword.

0000	1011	0101	1110
1000	0011	1101	0110

We then repeat steps 2 and 3 until we have completed all rows. We stop when we have reached 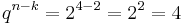$q^{n-k} = 2^{4-2} = 2^{2} = 4$ rows.

0000	1011	0101	1110
1000	0011	1101	0110
0100	1111	0001	1010
0010	1001	0111	1100

Note that in this example we could not have chosen the vector 0001 as the coset leader of the final row, even though it meets the critedia of having minimal weight (1), because the vector was already present in the array. We could, however, have chosen it as the first coset leader and constructed a different standard array.

Decoding via standard array

To decode a vector using a standard array, subtract the error vector - or coset leader - from the vector received. The result will be one of the codewords in $C$ . For example, say we are using the code C = {0000, 1011, 0101, 1110}, and have constructed the corresponding standard array, as shown from the example above. If we receive the vector 0110 as a message, we find that vector in the standard array. We then subtract the vector's coset leader, namely 1000, to get the result 1110. We have received the codeword 1110.

Decoding via a standard array is a form of nearest neighbour decoding. In practise, decoding via a standard array requires large amounts of storage - a code with 32 codewords requires a standard array with 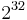$2^{32}$ entries. Other forms of decoding, such as syndrome decoding, are more efficient.

Note that decoding via standard array does not guarantee that all vectors are decoded correctly. If we receive the vector 1010, using the standard array above would decode the message as 1110, a codeword distance 1 away. However, 1010 is also distance 1 away from the codeword 1011. In such a case some implementations might ask for the message to be resent. This ambiguity is another reason that different decoding methods are sometimes used.

References

Hill, Raymond (1986). A First Course in Coding Theory. Oxford Applied Mathematics and Computing Science series. Oxford University Press. ISBN 9780198538035.